Securinets CTF 2018 Crypto Writeup

26 Mar, 2018

I’ve been looking for crypto challenges lately. In this CTF challenge, there are three crypto challenges (with some steganography for the last one).

Looser - 150 Points

We got flag.png.crypt, I think that this image may be encrypted with xor of some bytes. We know (by searching) that PNG file header starts its 8 bytes with 89 50 4E 47 0D 0A 1A 0A. So we try to find the key.

enc = open('flag.png.crypt').read()
heads = '89504E470D0A1A0A'.decode('hex')
ks = []
for i in range(8):
    ks += [ord(enc[i]) ^ ord(heads[i])]
print ks

The result is

[238, 238, 238, 238, 238, 238, 238, 238]

So we know that the key is just a single byte (with ordinal integer 238). After get the key we can xor the key with every bytes of encrypted image and get the flag.

enc = open('flag.png.crypt').read()
# 1st PNG byte
head = '89'.decode('hex')

def xor(a,b):
    return ''.join([chr(ord(x)^ord(y)) for x,y in zip(a,b)])

k = xor(enc[0],head)

dec = ''
for i in enc:
    dec += xor(k, i)

with open('flag.png', 'w') as f:
    f.write(dec)
    f.close()

And the flag is in the flag.png.

Flag: Flag{Hopefully_headers_are_constants}

The Worst RSA Joke - 350 Points

I was tried to find a way to factor its modular n, and all techniques I tried were failed. I decide to go back to the description and found that it uses single prime. Which means n is prime and I can’t factor it for sure. Back to the basic of RSA, we know that private key (d) is computed by

$$d \equiv e^{-1} \mod φ(n)$$

and we know that for any prime p, it holds

$$φ(p) = p-1$$

We have e and φ(n)(n-1),so we cat get the private key easily.

from Crypto.PublicKey import RSA
from Crypto.Util.number import long_to_bytes, bytes_to_long
from gmpy import invert
pubkey = RSA.importKey(open('public.pem').read())
p, e = pubkey.n, pubkey.e
c = bytes_to_long(open('flag.enc').read().decode('base64'))

d = invert(e, p-1)
m = pow(c, d, p)
flag = long_to_bytes(m)
print flag

And we get the output which contains our flag.

The empire secret system has been exposed ! The top secret flag is : Flag{S1nGL3_PR1m3_M0duLUs_ATT4cK_TaK3d_D0wn_RSA_T0_A_Sym3tr1c_ALg0r1thm}

Flag: Flag{S1nGL3_PR1m3_M0duLUs_ATT4cK_TaK3d_D0wn_RSA_T0_A_Sym3tr1c_ALg0r1thm}

Improve the quality - 800 Points

From the description, the secret message was splitted into parts (e.g. 123456 => 12, 34, 56). And each part is the secret key for each given point on the Elliptic Curve.

$$ Q1 = k1 * G \newline Q2 = k2 * G \newline … $$

We have to combine k1, k2, … to get the secret message.

1. Find B

With A, p, and (x,y) coordinate of any point on the curve, we can find B with

$$ y^2 \equiv x^3 + Ax + B\mod p\newline B \equiv y^2 - x^3 - Ax\mod p $$

I choose (x,y) from a generator G, compute above equation. We will get B as 618.

2. Find each secret key

Since it is just a small number, we can compute Discrete Logarithm directly via discrete_log in Sagemath.

#!/usr/bin/env sage 
A = 658974
p = 962280654317
B = Mod(339109212996**2 - 518459267012**3 - A*518459267012 , p)
E = EllipticCurve(GF(p), [A, B])
G = E(518459267012, 339109212996)

Qs = [(656055339629, 670956206845), 
(714432985374, 30697818482), 
(519532969453, 833497145865), 
(606806384185, 353033449641), 
(370553209582, 211121736115), 
(95617246846, 666814491609), 
(474872055371, 795112698430), 
(249845085299, 222352033875), 
(850954431245, 810446463695), 
(188731559428, 877002121896), 
(168665615402, 464872506873), 
(26722558561, 269217869309), 
(16403346294, 478534963882), 
(539749282946, 332444159141), 
(932295517649, 23439478940), 
(765194933041, 920187938377), 
(853124087439, 845601917928), 
(246454416048, 212483699689), 
(312547608490, 688107262695), 
(43261158649, 439444472742), 
(320785434805, 477080449838), 
(741706320740, 672809544395), 
(361762297756, 858805805323), 
(782235980044, 600673464737), 
(69196762074, 327427680437), 
(876001563166, 573218279075), 
(117946101727, 954797129239), 
(771781111553, 314018907599), 
(579549799021, 322325160055), 
(857081196493, 464260539273), 
(852938568103, 429083796488), 
(850954431245, 810446463695), 
(55203632714, 255470537391), 
(600464434215, 605840305721), 
(620532163623, 575613893944), 
(215810002861, 481354983411), 
(538481263994, 666638294130), 
(528666082457, 895034116069), 
(296218553972, 899557390183), 
(428618251485, 445768511836), 
(632412058600, 685699421425), 
(634041855232, 495546745721), 
(570481762204, 252944477333), 
(760959783781, 435626456209)]

Ks = []

for q in Qs:
    Q = E(q)
    Ks += [discrete_log(Q, G, operation='+')]

3. Find the (not really) fla

The hint said that after we get the key, split it to 2 chars (123456 => [12, 34, 56]) so I think that each element in the list can be transform with chr, and it is.

K = ''.join([str(i) for i in Ks])

flag = ''
for i in range(0,len(K),2):
    flag += chr(int(K[i:i+2]))

print flag

The output is

CONVERT THIS TO LOWER CASE FIRST :
THIS IMAGE CONTAINS THE FLAG, TRY TO GET IT
THE SUBMITTED FLAG MUST BE IN THIS FORMAT:
FLAG-EC[WHAT YOU'LL FIND IN THE IMAGE]
IMAGE URL:
HTTP://CRYPTO.CTFSECURINETS.COM/1/STEG-PART.PNG

Here is not the end. We need some more work to get the flag.

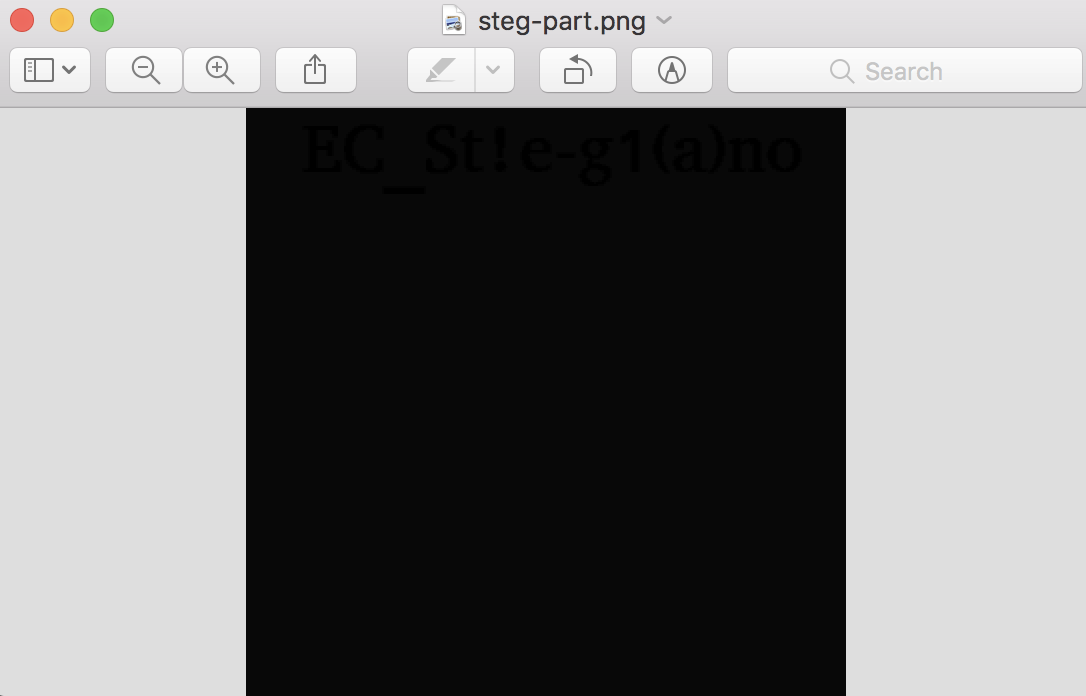
4. Play with Steg

After converting to the lower case and following the link, we get this image.

When it comes to steganography, I usually go to StegSolve as my first choice. And it doesn’t disappoints me.

Flag: flag-ec[EC_St!e-g1(a)no]