Mike's Marvelous Mystery Curves - TAMUCTF 2019 Writeup

05 Mar, 2019

Mike’s Marvelous Mystery Curves - 496 pts

In this challenge, we got a network traffic of the communication between two people, let’s call them Alice (192.168.11.4) and Bob (192.168.11.7). Besides, we know that the protocol they are using for key agreement is Eliptic Curve Diffie-Hellman. After analyzing the packet with the given information in the description, we can conclude each part of the packet into the picture below.

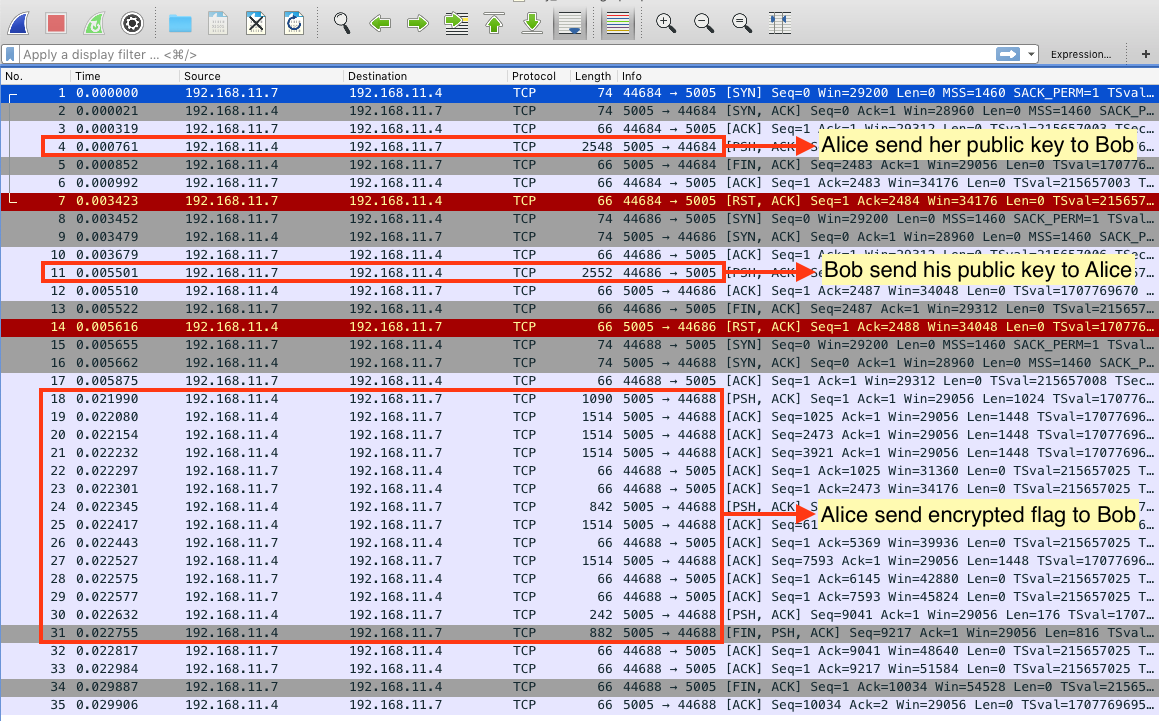
Look at the certificate packet Alice send to Bob.

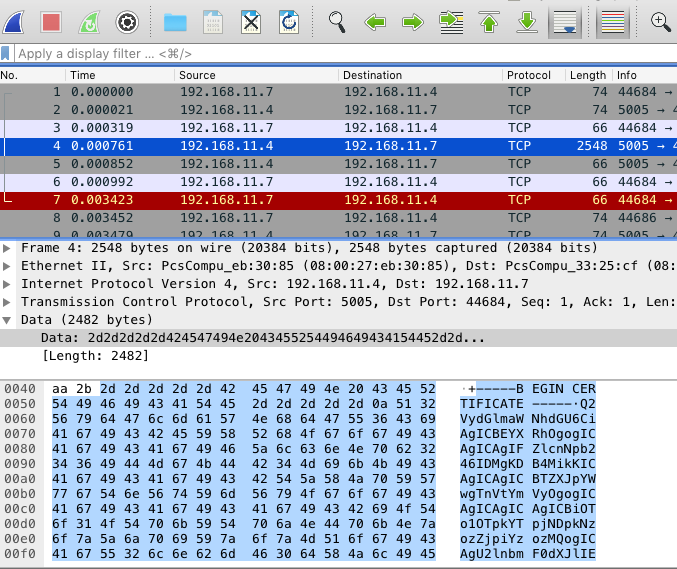
It’s a base64 encoded certificate. Without knowing what a format it is just try to decode base64 of the certificate. After decoding, We’ll see clear texts information about the public key with the parameter of custom elliptic curve parameters.

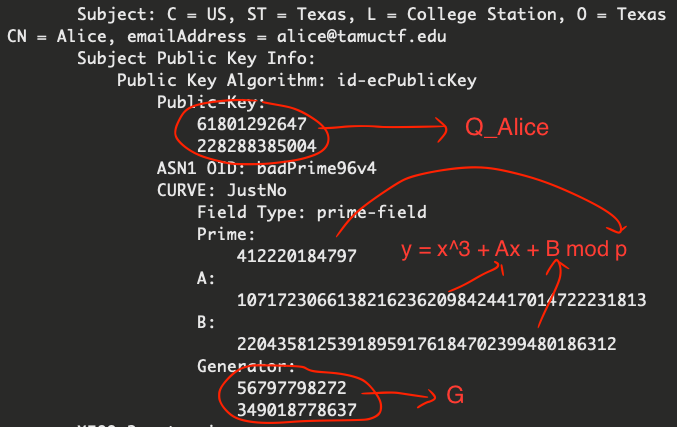
We can do the same thing with Bob’s certificate to get Bob’s public key.

We also see that the modulo prime number $p$ is very small (412220184797), so we can perform discrete logarithm to get the private keys of both Alice and Bob easily. In this case, I’ll use sagemath built-in discrete_log function.

What we gonna do to get the flag.

Perform ECDH discrete logarithm to get private keys of Alice and Bob, then compute shared key.
Decrypt the traffic data with shared key.

For the encrypted data part, I just copied all the encrypted data as hex streams and save it in data.txt, since there are only few packets, copy-and-paste can makes the job done.

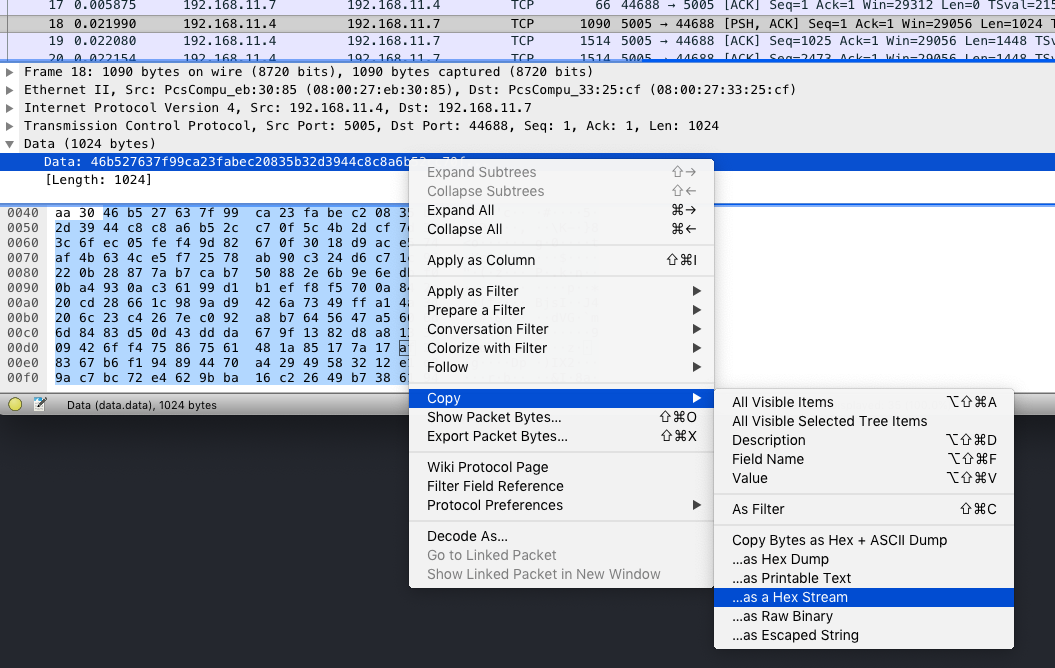
We will compute shared key by computing $d_{Alice} * d_{Bob} * G$, then decrypt these data with AES-CBC-192 according to the challenge description.

#!/usr/bin/env sage
from Crypto.Cipher import AES

p = 412220184797
A = 10717230661382162362098424417014722231813
B = 22043581253918959176184702399480186312
E = EllipticCurve(GF(p), [A, B])
G = E(56797798272, 349018778637)

Q_Alice = E(61801292647, 228288385004)
Q_Bob = E(196393473219, 35161195210) 

# perform discrete logarithm
# can use built-in "discrete_log", since "p" is very small
d_Alice = G.discrete_log(Q_Alice) # Q_Alice = d_Alice * G
d_Bob = G.discrete_log(Q_Bob) # Q_Bob = d_Bob * G

shared_key = d_Alice * d_Bob * G
(x,y,_) = shared_key
key = '{}{}'.format(x, y) # according to the problem description

cipher = AES.new(key, mode=AES.MODE_CBC, IV='\x00'*16) # AES-CBC-192
enc = ''.join(open('data.txt').read().split('\n'))
flag = cipher.decrypt(enc.decode('hex'))
print flag

The result is the content of the book, “The Hitchhiker’s Guide to the Galaxy”, with the flag inside.

Flag: gigem{Forty-two_said_Deep_Thought}